Tính chất, công thức tính đường trung tuyến là gì?
Đường trung tuyến là kiến thức thuộc môn hình học của bậc học trung học, nó chủ yếu được áp dụng trong tam giác. Việc biết được định nghĩa, tính chất cũng như công thức tính sẽ giúp bạn áp dụng để giải quyết các bài toán dễ dàng. Vậy đường trung tuyến là gì? Cùng chúng tôi tìm hiểu về đường trung tuyến ngay sau đây nhé.
Đường trung tuyến là gì?
Đường trung tuyến là gì là nghi vấn của không ít người. Theo Wikipedia, đường trung tuyến của đoạn thẳng chính là đường thẳng đi qua trung điểm của đoạn thẳng đó.
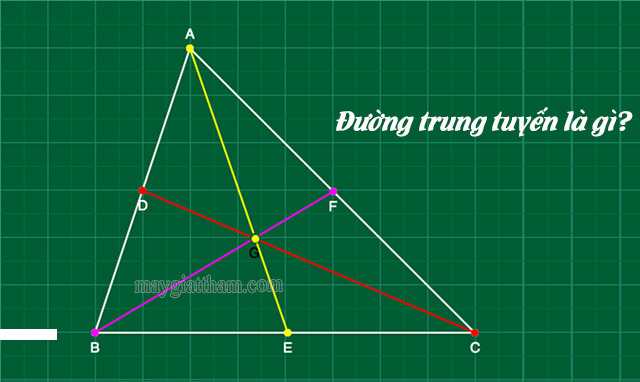
Trong hình học, đường trung tuyến của một tam giác chính là một đoạn thẳng nối từ đỉnh của tam giác đến trung điểm của cạnh đối diện. Mỗi tam giác sẽ có ba trung tuyến.
Tính chất của đường trung tuyến là gì?
Tính chất của đường trung tuyến rất quan trọng, nhất là trong hình học tam giác. Bằng cách nắm được các tính chất của đường trung tuyến, chúng ta có thể hiểu sâu hơn về cấu trúc cũng như các mối quan hệ trong tam giác. Đường trung tuyến của mỗi loại tam giác sẽ có một số tính chất đặc biệt như sau.
Tính chất đường trung tuyến tam giác thường
- Ba đường trung tuyến của một tam giác sẽ cùng đi qua một điểm.
- Giao điểm của ba đường trung tuyến trong tam giác được gọi là trọng tâm.
- Trọng tâm của một tam giác sẽ cách đỉnh một khoảng bằng 2/3 độ dài của đường trung tuyến đi qua đỉnh ấy.
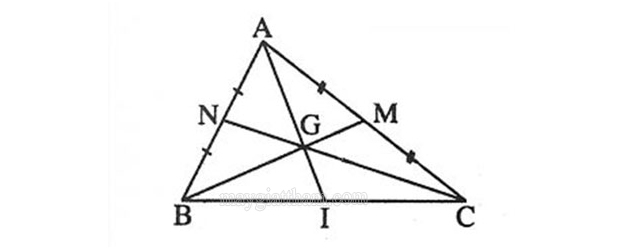
Ví dụ: Gọi G chính là trọng tâm của tam giác ABC. Tam giác ABC có các trung tuyến là AI, BM, CN thì ta sẽ có biểu thức: =
=
=
.
Đường trung tuyến tam giác vuông
- Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền sẽ bằng
cạnh huyền.
- Một tam giác mà có đường trung tuyến ứng với một cạnh và bằng nửa cạnh đó thì tam giác này là tam giác vuông.
- Đường trung tuyến của tam giác vuông có đầy đủ những tính chất của một đường trung tuyến tam giác.
Ví dụ: Cho tam giác vuông ABC, có AD là đường trung tuyến ứng với cạnh huyền BC. => AD = BC = DB = DC.
Ngược lại, nếu trung tuyến AD = BC thì ABC là tam giác vuông tại A.
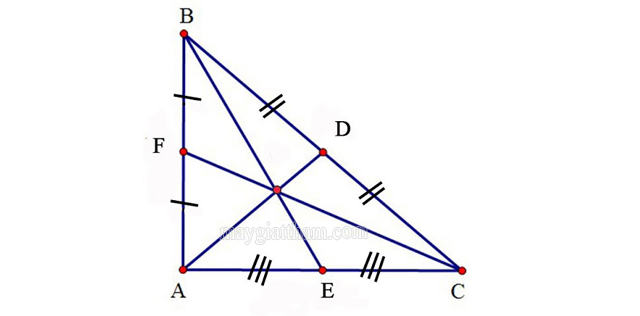
Đường trung tuyến tam giác cân
- Trong một tam giác cân, đường trung tuyến ứng với cạnh đáy thì sẽ vuông góc với cạnh đáy. Và chia tam giác cân thành 2 tam giác bằng nhau.
Ví dụ: Tam giác ABC cân tại A, có đường trung tuyến AD ứng với cạnh BC=> AD ⊥ BC và tam giác ADB = tam giác ADC.
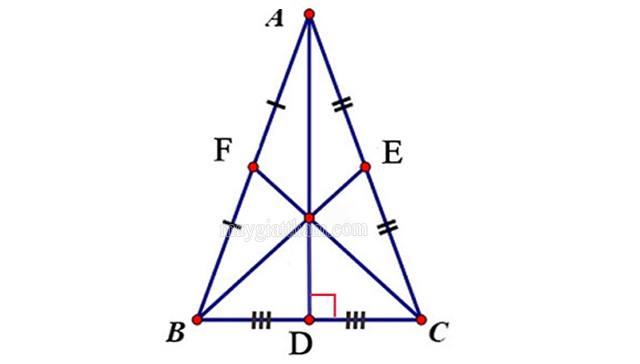
Đường trung tuyến tam giác đều
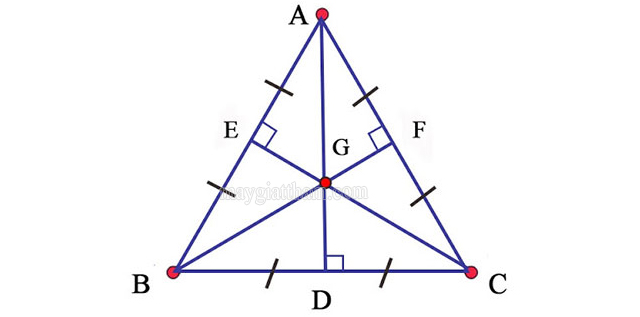
- Trong 1 tam giác đều, 3 đường trung tuyến sẽ chia tam giác đó thành 6 tam giác nhỏ có diện tích bằng nhau.
- Trong một tam giác đều, đường thẳng đi qua một đỉnh bất kỳ và đi qua trọng tâm của tam giác thì sẽ chia tam giác đó thành 2 tam giác có diện tích bằng nhau.
Ví dụ: Tam giác đều ABC có trung tuyến AD, BF, CE => ΔGAF = ΔGAE = ΔGCF = ΔGCD = ΔGBD = ΔGEB = ΔGBE = ΔGEA
SΔADB = SΔADC = SΔCEA = SΔCEB = SΔBFA = SΔBFC
Công thức tính chiều dài đường trung tuyến của tam giác
Độ dài của đường trung tuyến trong một tam giác sẽ được tính thông qua độ dài của các cạnh tam giác và được tính theo định lý Apollonnius. Theo đó ta có:
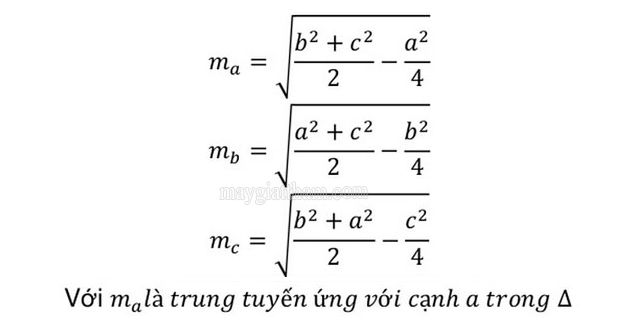
Trong đó:
- a, b, c: là các cạnh của tam giác.
- ma, mb, mc: là những đường trung tuyến của tam giác.
Bài tập về đường trung tuyến
Tham khảo một số bài tập về đường trung tuyến để nắm chắc hơn về kiến thức này nhé.
Bài tập 1: Cho tam giác ABC có hai đường trung tuyến là BM và CN cắt nhau tại điểm G. Trên tia GB và GC hãy lấy các điểm F và E sao cho G chính là trung điểm của FM đồng thời cũng là trung điểm của EN. Chứng minh rằng ba đường thẳng AG, BE, CF đồng quy.
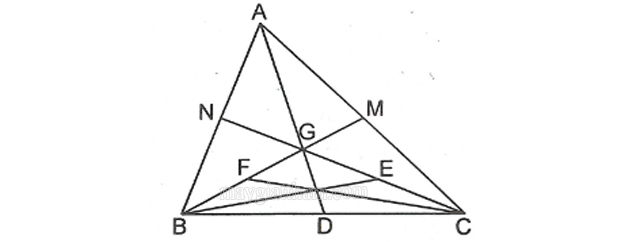
Gợi ý lời giải: Để chứng minh ba đường thẳng AG, BE và CF đồng quy ta có thể chứng minh đây là ba đường trung tuyến của tam giác GBC.
Gọi D chính là giao điểm của AG và BC. Vì G là trọng tâm của ΔABC nên AD là đường trung tuyến, => DB = DC.
Ta có GF = GM = BM; GE = GN =
CN
Do đó, GF = FB (=BM)’ GE = EC (=
CN)
Xét ΔGBC có GD, BE, CF là ba đường trung tuyến, cho nên chúng đồng quy. => ba đường thẳng là AD, BE, CF đồng quy.
Bài tập 2: Cho ΔABC có BC = a = 10 cm, CA = b = 8 cm, AB = c = 7 cm. Tính độ dài của các đường trung tuyến của Δ ABC.
Gợi ý lời giải: Gọi độ dài các đường trung tuyến từ các đỉnh A, B, C của ΔABC lần lượt là ma; mb; mc. Áp dụng công thức tính chiều dài đường trung tuyến ta có:
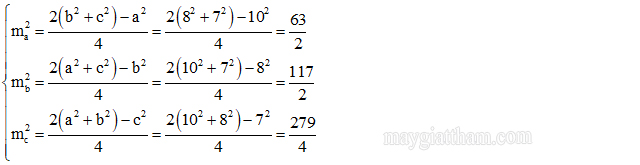
Vì độ dài đường trung tuyến luôn dương, do đó:

Trên đây là tổng hợp những thông tin giải đáp nghi vấn đường trung tuyến là gì? Những tính chất của đường trung tuyến này rất quan trọng nên bạn cần nắm chắc nhé.
The post Tính chất, công thức tính đường trung tuyến là gì? appeared first on Máy giặt thảm- Máy hút bụi công nghiệp chính hãng giá rẻ.
from Máy giặt thảm- Máy hút bụi công nghiệp chính hãng giá rẻ https://ift.tt/dBfQeoG

Nhận xét
Đăng nhận xét